From README.txt
RSBench is mini-app to represent the multipole resonance representation lookup cross section algorithm for Monte Carlo neutron transport.
Problem Size Discussion
From README.txt
Problem size should be scaled using the -p <particles> parameter. The default is set to 300,000, but full application runs may use up to several billion particles per generation.
Analysis
RSBench was compute bound on the Skylake machine that this analysis was run on and spent 27.1% of its time in libm.
Build and Run Information
Compiler = icc (ICC) 18.0.1 20171018
Build_Flags = -std=gnu99 -g -O3 -qopenmp -march=skylake-avx512 \
-mtune=skylake-avx512 -ansi-alias -no-prec-div
Run_Parameters = -p 1000000 -t <# of Threads>
Scaling
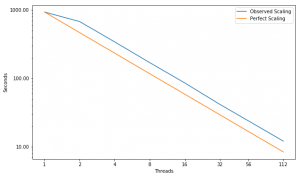
Performance Improvement
| Threads |
2 |
4 |
8 |
16 |
32 |
56 |
112 |
| Speed Up |
1.38X |
1.99X |
2.01X |
1.99X |
2.06X |
1.74X |
1.99X |
Hit Locations
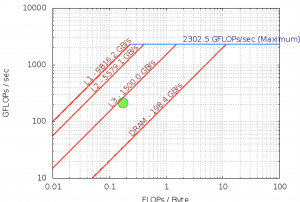
FLOPS
| Double Precision |
Scalar |
128B Packed |
256B Packed |
512B Packed |
Total FLOPS |
GFLOPS/sec |
| PMU |
5.090e+11 |
1.970e+12 |
1.780e+11 |
0.000e+00 |
5.161e+12 |
2.157e+02 |
| SDE |
2.898e+11 |
1.004e+12 |
8.096e+10 |
0.000e+00 |
2.621e+12 |
1.095e+02 |
Intel Software Development Emulator
| Intel SDE |
RSBench |
| Arithmetric Intensity |
0.175 |
| FLOPS per Inst |
0.83 |
| FLOPS per FP Inst |
1.91 |
| Bytes per Load Inst |
12.1 |
| Bytes per Store Inst |
13.0 |
Roofline – Intel(R) Xeon(R) Platinum 8180M CPU
112 Threads – 56 – Cores 3200.0 Mhz
UOPS Executed
Memory Footprint
| Maximum Resident Set Size |
MBytes |
| 1 Thread |
44.89 MB |
| 56 Thread |
188.18 MB |
| 112 Thread |
196.52 MB |
Experiment Aggregate Metrics
| Threads (Time) |
IPC per Core |
Loads per Cycle |
L1 Hits per Cycle |
L1 Miss Ratio |
L2 Miss Ratio |
L3 Miss Ratio |
L2 B/W Utilized |
L3 B/W Utilized |
DRAM B/W Utilized |
| 1 (100.0%) |
1.39 |
0.85 |
0.80 |
1.17% |
60.00% |
0.55% |
2.35% |
8.71% |
9.69% |
| 56 (100.0%) |
1.95 |
0.60 |
0.57 |
1.59% |
52.25% |
0.14% |
3.20% |
15.69% |
79.85% |
| 112 (100.0%) |
1.93 |
0.60 |
0.57 |
1.59% |
52.05% |
0.32% |
3.17% |
15.54% |
77.54% |
calculate_micro_xs_doppler
| Threads (Time) |
IPC per Core |
Loads per Cycle |
L1 Hits per Cycle |
L1 Miss Ratio |
L2 Miss Ratio |
L3 Miss Ratio |
L2 B/W Utilized |
L3 B/W Utilized |
DRAM B/W Utilized |
| 1 (98.5%) |
1.39 |
0.85 |
0.79 |
1.18% |
60.59% |
0.55% |
2.35% |
8.63% |
9.56% |
| 56 (96.0%) |
1.94 |
0.59 |
0.56 |
1.65% |
52.55% |
0.14% |
3.22% |
15.41% |
78.73% |
| 112 (96.9%) |
1.92 |
0.58 |
0.55 |
1.66% |
52.40% |
0.31% |
3.16% |
15.19% |
76.14% |
152 // Temperature Dependent Variation of Kernel
153 // (This involves using the Complex Faddeeva function to
154 // Doppler broaden the poles within the window)
155 void calculate_micro_xs_doppler( double * micro_xs, int nuc, double E, Input input,
CalcDataPtrs data, complex double * sigTfactors,
long * abrarov, long * alls)
156 {
157 // MicroScopic XS's to Calculate
158 double sigT;
159 double sigA;
160 double sigF;
161 double sigE;
162
163 // Calculate Window Index
164 double spacing = 1.0 / data.n_windows[nuc];
165 int window = (int) ( E / spacing );
166 if( window == data.n_windows[nuc] )
167 window--;
168
169 // Calculate sigTfactors
170 calculate_sig_T(nuc, E, input, data, sigTfactors );
171
172 // Calculate contributions from window "background"
// (i.e., poles outside window (pre-calculated)
173 Window w = data.windows[nuc][window];
174 sigT = E * w.T;
175 sigA = E * w.A;
176 sigF = E * w.F;
177
178 double dopp = 0.5;
179
180 // Loop over Poles within window, add contributions
181 for( int i = w.start; i < w.end; i++ )
182 {
183 Pole pole = data.poles[nuc][i];
184
185 // Prep Z
186 double complex Z = (E - pole.MP_EA) * dopp;
187 if( cabs(Z) < 6.0 )
188 (*abrarov)++;
189 (*alls)++;
190
191 // Evaluate Fadeeva Function
192 complex double faddeeva = fast_nuclear_W( Z );
193
194 // Update W
195 sigT += creal( pole.MP_RT * faddeeva * sigTfactors[pole.l_value] );
196 sigA += creal( pole.MP_RA * faddeeva);
197 sigF += creal( pole.MP_RF * faddeeva);
198 }
199
200 sigE = sigT - sigA;
201
202 micro_xs[0] = sigT;
203 micro_xs[1] = sigA;
204 micro_xs[2] = sigF;
205 micro_xs[3] = sigE;
206 }
[I] calculate_sig_T
| Threads (Time) |
IPC per Core |
Loads per Cycle |
L1 Hits per Cycle |
L1 Miss Ratio |
L2 Miss Ratio |
L3 Miss Ratio |
L2 B/W Utilized |
L3 B/W Utilized |
DRAM B/W Utilized |
| 1 (36.0%) |
1.42 |
0.67 |
0.66 |
0.84% |
25.33% |
0.17% |
0.90% |
1.36% |
0.89% |
| 56 (31.3%) |
2.05 |
0.49 |
0.48 |
1.18% |
32.79% |
1.99% |
2.21% |
7.02% |
42.16% |
| 112 (31.7%) |
2.04 |
0.49 |
0.48 |
1.19% |
32.46% |
4.54% |
2.14% |
7.00% |
40.31% |
208 void calculate_sig_T( int nuc, double E, Input input, CalcDataPtrs data,
complex double * sigTfactors )
209 {
210 double phi;
211
212 for( int i = 0; i < input.numL; i++ )
213 {
214 phi = data.pseudo_K0RS[nuc][i] * sqrt(E);
215
216 if( i == 1 )
217 phi -= - atan( phi );
218 else if( i == 2 )
219 phi -= atan( 3.0 * phi / (3.0 - phi*phi));
220 else if( i == 3 )
221 phi -= atan(phi*(15.0-phi*phi)/(15.0-6.0*phi*phi));
222
223 phi *= 2.0;
224
225 sigTfactors[i] = cos(phi) - sin(phi) * _Complex_I;
226 }
227 }
Time Spent in Math Functions
| Function |
% Time |
__libm_sse2_sincos |
15.1 % |
__libm_atan_l9 |
8.0 % |
__svml_sincos4_z0 |
3.8 % |
[I] fast_nuclear_W
| Threads (Time) |
IPC per Core |
Loads per Cycle |
L1 Hits per Cycle |
L1 Miss Ratio |
L2 Miss Ratio |
L3 Miss Ratio |
L2 B/W Utilized |
L3 B/W Utilized |
DRAM B/W Utilized |
| 1 (18.3%) |
1.34 |
1.03 |
0.93 |
1.05% |
68.17% |
0.18% |
3.04% |
10.73% |
15.28% |
| 56 (16.6%) |
1.85 |
0.53 |
0.48 |
1.75% |
63.70% |
0.07% |
3.70% |
17.91% |
90.18% |
| 112 (16.8%) |
1.84 |
0.54 |
0.49 |
1.73% |
63.39% |
0.16% |
3.60% |
17.25% |
86.14% |
3 // This function uses a combination of the Abrarov Approximation
4 // and the QUICK_W three term asymptotic expansion.
5 // Only expected to use Abrarov ~0.5% of the time.
6 double complex fast_nuclear_W( double complex Z )
7 {
8 // Abrarov
9 if( cabs(Z) < 6.0 )
10 {
11 // Precomputed parts for speeding things up
12 // (N = 10, Tm = 12.0)
13 double complex prefactor = 8.124330e+01 * I;
14 double an[10] = {
15 2.758402e-01,
16 2.245740e-01,
17 1.594149e-01,
18 9.866577e-02,
19 5.324414e-02,
20 2.505215e-02,
21 1.027747e-02,
22 3.676164e-03,
23 1.146494e-03,
24 3.117570e-04
25 };
26 double neg_1n[10] = {
27 -1.0,
28 1.0,
29 -1.0,
30 1.0,
31 -1.0,
32 1.0,
33 -1.0,
34 1.0,
35 -1.0,
36 1.0
37 };
38
39 double denominator_left[10] = {
40 9.869604e+00,
41 3.947842e+01,
42 8.882644e+01,
43 1.579137e+02,
44 2.467401e+02,
45 3.553058e+02,
46 4.836106e+02,
47 6.316547e+02,
48 7.994380e+02,
49 9.869604e+02
50 };
51
52 double complex W = I * ( 1 - fast_cexp(I*12.*Z) ) / (12. * Z );
53 double complex sum = 0;
54 for( int n = 0; n < 10; n++ )
55 {
56 complex double top = neg_1n[n] * fast_cexp(I*12.*Z) - 1.;
57 complex double bot = denominator_left[n] - 144.*Z*Z;
58 sum += an[n] * (top/bot);
59 }
60 W += prefactor * Z * sum;
61 return W;
62 }
63
64 // QUICK_2 3 Term Asymptotic Expansion (Accurate to O(1e-6)).
65 // Pre-computed parameters
66 double a = 0.512424224754768462984202823134979415014943561548661637413182;
67 double b = 0.275255128608410950901357962647054304017026259671664935783653;
68 double c = 0.051765358792987823963876628425793170829107067780337219430904;
69 double d = 2.724744871391589049098642037352945695982973740328335064216346;
70
71 // Three Term Asymptotic Expansion
72 double complex W = I * Z * (a/(Z*Z - b) + c/(Z*Z - d));
73
74 return W;
75 }



