ASPA

From aspa.pdf

The purpose of ASPA (Adaptive Sampling Proxy Application) is to enable the evaluation of a technique known as adaptive sampling on advanced computer architectures. Adaptive sampling is of interest in simulations involving multiple physical scales, wherein models of individual scales are combined using some form of scale bridging.

Adaptive sampling [Barton2008,Knap2008] attempts to significantly reduce the number of fine-scale evaluations by dynamically constructing a database of fine-scale evaluations and interpolation models. When the response of the fine-scale model is needed at a new point, the database is searched for interpolation models centered at ‘nearby’ points. Assuming that the interpolation models possess error estimators, they can be evaluated to determine if the fine-scale response at the current query point can be obtained to sufficient accuracy simply by interpolation from previously known states. If not, the fine-scale model must be evaluated and the new input/response pair added to the closest interpolation model.

##

Build and Problem Configuration
ASPA is run by executing:

./aspa point_data.txt value_data.txt

The parameter file aspa.inp is automatically read:

aspa.inp

maxKrigingModelSize 4
maxNumberSearchModels 4
theta 1.2e3
meanErrorFactor 1.0
tolerance 1.0e-7
maxQueryPointModelDistance 1.0e3

##

Analysis

Build and Run Information

Compiler = icpc (ICC) 18.0.1 20171018
Build_Flags = -g -O3 -march=native -std=c++0x -llapack -lblas
Run_Parameters = point_data.txt value_data.txt

Run on 1 Thread on 1 Node

Intel Software Development Emulator

| SDE Metrics |

ASPA|
|:———–|:—:|
| Arithmetic Intensity | 0.06 |
| Bytes per Load Inst | 7.89 |
| Bytes per Store Inst | 8.28 |

Roofline – Intel(R) Xeon(R) CPU E5-2699 v3 @ 2.30GHz

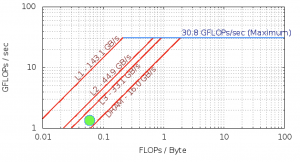
ASPA makes use of a database (M-tree database), however the sparse data interpolation (known as kringing) takes the vast of the application cycles. The I/O involved is not significant.

The code that is performing the bulk of the work (81.1%) is in the BLAS library within the following kernels:

|BLAS Function|

% Cycles |
|:————|:——–:|
|dgemv | 59.4% |
|dgemm | 15.3% |
|dtrsm | 5.2% |
|ddot | 1.1% |
The calls to the BLAS kernels primarily originate from the following loop in the MultivariateDerivativeKringingModel::getMeanSquaredError:

1462 for (int i = 0; i < valueDimension; ++i) {
1463
1464 //
1465 // initialize with the self correlation term
1466 //
1467
1468 errorVector[i] = sigma[i][i];
1469
1470 //
1471 // add u.(XVX)^-1.u^T contribution
1472 //
1473
1474 getRow(uRow,
1475 u,
1476 i);
1477
1478 errorVector[i] += dot(uRow,
1479 mult(_matrixInverseXVX, uRow));
1480
1481 //
1482 // add r^T V^-1 r contribution
1483 //
1484
1485 getColumn(rColumn,
1486 r,
1487 i);
1488
1489 errorVector[i] -= dot(rColumn,
1490 mult(_matrixInverseV, rColumn));
1491
1492 //
1493 // apply self-correlation
1494 //
1495
1496 errorVector[i] *= _sigmaSqr[valueId];
1497
1498 }

Experiment Aggregate Metrics

|

IPC per Core |
Loads per Cycle |
L1 Hits per Cycle |
L1 Miss Ratio |
L2 Miss Ratio |
L3 Miss Ratio |
L2 B/W Utilized |
L3 B/W Utilized |
|:—:|:—:|:—:|:—:|:—:|:—:|:—:|:—:|
|2.63|0.91|1.06|2.77%|4.61%|6.55%|9.60%|1.14%|

DGEMV (Level 2)

|

IPC per Core |
Loads per Cycle |
L1 Hits per Cycle |
L1 Miss Ratio |
L2 Miss Ratio |
L3 Miss Ratio |
L2 B/W Utilized |
L3 B/W Utilized |
|:—:|:—:|:—:|:—:|:—:|:—:|:—:|:—:|
|2.57|1.03|1.02|3.36%|2.02%|8.45%|11.39%|0.48%|

DGEMM (Level 3)

|

IPC per Core |
Loads per Cycle |
L1 Hits per Cycle |
L1 Miss Ratio |
L2 Miss Ratio |
L3 Miss Ratio |
L2 B/W Utilized |
L3 B/W Utilized |
|:—:|:—:|:—:|:—:|:—:|:—:|:—:|:—:|
|3.90|1.05|1.54|0.43%|6.71%|12.41%|2.46%|0.74%|